2 - Calcul du coefficient Cx
Vous pouvez visionner cette vidéo qui reprend l'ensemble de l'étude avec quelques points supplémentaires.
|
|---|
Définition : Source Wikipédia :
Le coefficient de traînée Cx est défini par :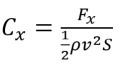 
où :
Fx est la force de traînée, qui est par définition la composante de la force dans la direction du vecteur vitesse,
ρ est la masse volumique du fluide,
v est la vitesse de l'objet relativement au fluide,
S est la surface de référence.
La masse volumique et la vitesse sont prises à l'infini amont (ou en tous cas loin de toute perturbation locale due à l'obstacle). Nota : on reconnait au dénominateur la pression dynamique Pdyn donnée par :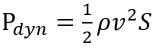 
La surface de référence est une surface choisie arbitrairement, souvent celle du maître-couple, projection du solide sur un plan perpendiculaire au déplacement, sauf dans le cas des ailes en aéronautique, pour lesquelles on rapporte les forces à la surface alaire, projection des ailes sur un plan contenant la corde des profils, ce qui permet de comparer des profils indépendamment de leur épaisseur. Néanmoins pour des études particulières, d'autres surfaces de référence peuvent être utilisées.
Méthode :
Question 1 - Sur votre compte rendu, déterminer la relation permettant de calculer Cx fonction de Fz, ρ, V et S.
Question 2 - Sur SolidWorks, relever l'aire en m² de surface projetée en suivant l'aide suivante :
Revenir au modèle du bloc. Créer une nouvelle esquisse suivant le plan de face.- Sélectionner Convertir les entités , puis cliquer sur les contours a projeter. Vous pouvez vous limiter au contours du bloc principal.
Attention :
L'esquisse doit être un contour fermé comme pour une fonction d'extrusion ou de révolution.
Méthode :
- Dans le menu supérieur, sélectionner l'onglet évaluer puis Propriétés de la section.
- Sélectionner l'esquisse et Calculer. Vous pouvez changer les unités dans Options.
Question 3 - Calculer le coefficient Cx du bloc d’origine en détaillant vos calculs. Attention aux unités, elles doivent être uniformes.