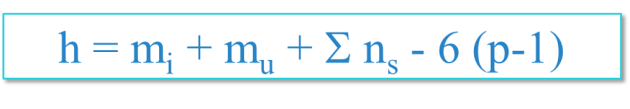HYPERSTASTISME D'UN SYSTÈME
Fondamental :
En mécanique du solide, l'hyperstatisme est la situation d'un assemblage pour lequel le fonctionnement se fait avec plus de contraintes que ce qui est strictement nécessaire pour le maintenir, ce qui signifie qu'au moins un degré de mobilité d'une pièce est supprimé plusieurs fois.
À l'inverse, on parle d'isostatisme lorsque le fonctionnement se fait sans contrainte excessive ou pour être plus rigoureux si le principe fondamental de la dynamique suffit à déterminer toutes les inconnues de liaisons du mécanisme. Ainsi, la mobilité d'une pièce d'un assemblage est nécessairement limitée ; certains degrés de mobilité sont supprimés, mais chaque degré de mobilité n'est supprimé qu'une seule fois.
On parle également d'hypostatisme lorsque l'assemblage possède trop de mobilités. D'un point de vue mécanique, au moins une pièce conserve au moins une possibilité de mouvement (au moins un degré de mobilité) qui est nuisible au fonctionnement. Si c'est un mécanisme, il va présenter des instabilités, des mouvements parasites ; si c'est une charpente, elle ne tiendra pas.
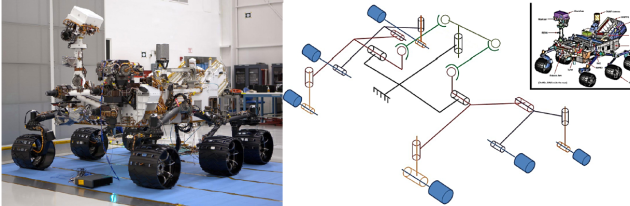
Sonde spatiale ‘'rover curiosity'', mécanisme réel et schéma cinématique spatiale
Méthode : CALCUL DU DEGRÉ D'HYPERSTASTISME
mi = mobilités internes
mu = mobilités utiles
Σ ns = somme des inconnues statiques de chaque liaison.
p = Nombre de CE
Définition :
si h = 0 , il y a autant d'équations que d'inconnues, on peut donc déterminer tous les efforts, c'est l'isostatisme ;
si Ns < 0 , on a plus d'équations que d'inconnues, ce qui signifie les efforts ne sont pas définis en statique, donc qu'il y a des mouvements possibles qui nuisent à ce qui a été « planifié », à la fonctionnalité du système ; c'est l'hypostatisme ;
si Ns >0 , on a plus d'inconnues que d'équations, il est impossible de calculer tous les efforts avec la statique ; c'est l'hyperstatisme.
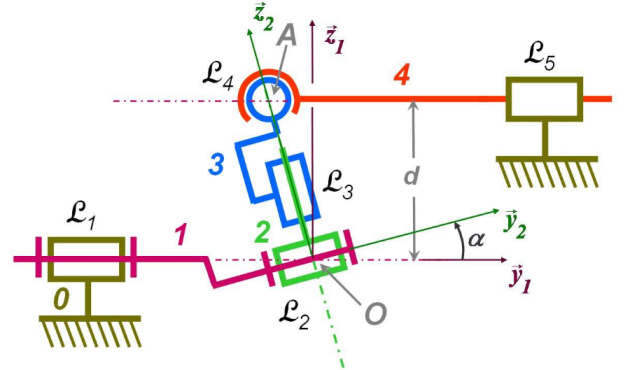
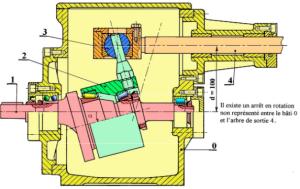
Exemple : CAPSULEUSE DE BOUTEILLES
mi = 1 : mobilités du solide 3 qui tourne librement autour des axes (O,z2) mu = 1 : loi entrée/sortie du mécanisme p = 5 : 5 classes d'équivalence Σ ns = somme des inconnues statiques de chaque liaison.
|  |
h = mi + mu + Σns + 6 (p-1)
h = 1 + 1 + 22 - 6(5-1) =0
